Announcing the launch of my newest Flash game, TriGaVoid, posted over at Kongregate. You can play TriGaVoid here.
Tag: Flash
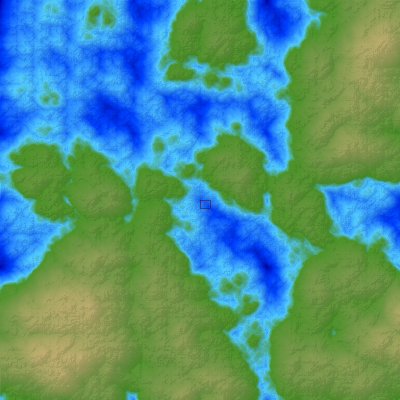
Procedurally Generated Map With Shading
Click here to load the map. Once it launches, click the movie to activate it, then use the arrow keys to move around. Clicking “reset” will create a new map.
This is a quick update to the tile game experiments of days past. I worked up a better color palette, and figured out a way to include shading to provide a better sense of depth and scale.
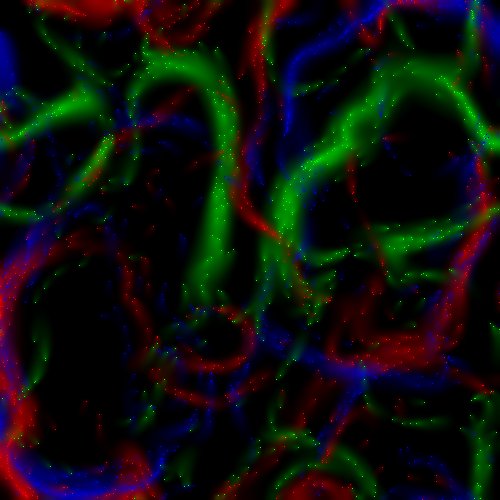
Perlin Ants In Color
Click here to launch the ants.
Click the left button to reset the terrain which the ants follow.
Click the right button to show and hide the terrain.
1800 ants in a full-color version of yesterday’s experiment. Instead of looking for dark/light pixels, the ants look at the different color channels of the pixel they land on – red, green and blue. Then the ants follow the same pattern as yesterday – dark pixels turn left, light pixels turn right – based on the intensity of the target color.
Yup. I like how this one turned out, too.
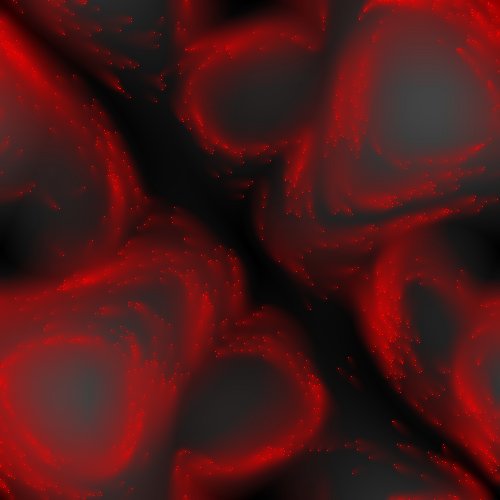
Perlin Ants
Click here to launch the ants.
Click the left square to generate a new terrain map.
Click the right square to show and hide the terrain map.
This is kind of a mash-up between bits and pieces of some previous experiments – the terrain from the tile-based game, and the ants from the Langton’s Ants experiments.
Basically, what is happening here is this: A thousand “ants” are created and placed in random locations on the screen, facing in random directions. Each turn, each ant moves forward one pixel. If the color of the new pixel is lighter than the previous pixel, it turns a bit widdershins. If the new pixel is darker, it turns a bit clockwise.
The ants end up tracing something like contour lines, and seem to be “attracted” to sections where the color of the terrain varies significantly over a small area.
I threw in a bit of a blur to make things more interesting visually.
Enjoy!
Tile Game With Location Detection
Click here to launch the game.
Click anywhere in the prototype to bring it into focus, then use the arrow keys to move. For a detailed explanation of what is going on, read my GameDev.net blog post.
Tile-based Game Engine update
Click here to launch the experiment
.
This is a small update to an experiment I have been working on, off and on, over the past several months. Click on the Flash movie to bring it into focus, then use the cursor keys to move around.
Gyruss Play-ability Update
Click the movie to bring the game into focus; LEFT and RIGHT keys to move, SPACE to fire.
Langton’s Ant 3D, Version 2
Another Langton’s Ant 3D experiment. Click here to run the experiment.
I finally got the ruleset sorted out, and now I have a simple 3d version of Langton’s Ant up and running. This is how it works:
Remember the behavior of Langton’s Ant:
1. If the ant is on an empty cell, color it in and move according to the next rule in the set.
2. If the ant is on a filled cell, empty the cell and move according to the previous rule in the set.
3. Do not talk about fight club.
The space in which the Ant is moving is a 50x50x50 (125,000) grid of cells.
There are eight rules which the ant follows, which – if none of the cells are colored in yet – the ant will follow in sequence:
1. Z–
2. X++
3. Y++
4. X–
5. Z++
6. X++
7. Y–
8. X–
In non-computerese, when the applet first runs, the ant will travel in, right, down, left, out, right, up, left, and in doing so fill in eight cells which make up a 2x2x2 cube.
2-3
5-4
1-8
6-7
With the next step the ant begins to encounter filled cells, which mean it takes a step back in the ruleset, and perhaps another, and eventually start to travel to new cells.
It is important, in order for the ant to make the desired patterns, that the sequence of movements in the ruleset visit each cell in a cube of cells exactly once, with the next iteration through the ruleset returning the ant to the original cell. Also, no diagonal movement; only cell face to cell face. I am not sure if this can be accomplished with more than a 2x2x2 cube.
In this demo the cells are colored in according to the “depth”, or the Z value of the cell-s position. Cells farther in the “back” are blue, and cells closer to the “front” are red. All layers (Z) are faded back except for the layer in which the Ant is currently moving. This is why there appears to be a “screen” of cells which moves back and forth and changes colors constantly.
Also in this demo, the pattern created appears to trend to the lower right corner of the screen because each of the layers, back to front, has been offset one cell to the right and one cell down, to provide a sort of isometric view of the pattern.
More experiments along these lines to come, after my brain cools down a bit.
Langton’s Ant 3D, Version 1
Click here to see the ant in new amazing 3D action.
My first attempt at moving Langton’s Ant into a 3D grid. The 3D part was easy – just add some Z movement to the existing X and Y pattern.
This is what you are looking at: there are 100 cells in the X (left and right) and Y (up and down) plane, and 25 in the Z (toward and away from the viewer) plane. There is one bitmap for each Z level, making for 25 stacked bitmaps. The bitmap in which the ant is currently moving is set at 100% opacity, with the surrounding bitmaps becoming increasingly opaque until they are almost transparent. When the experiment seems to flicker, it is because the ant is rapidly switching between Z levels. Those long horizontal “roads” the ant makes are probably more like tubes when viewed in 3D space.
Making the ant move in an interesting pattern is a little more difficult. In 2D (X,Y) space, from each point the ant can either turn left or right, and move forward one space, depending on the state of the cell to which the ant moves. That means, using initial conditions, the ant will move in a perfect square: up 1, left 1, down 1, right 1, and end up back at the original square. In order for me to make that work in 3D space, the ant must visit each of eight cells, forming a cube, and return to the original cell without doubling back on itself. The current experiment does not do that, thus the long horizontal runs.
Right now there are 18 rules for the ant’s movements. Each of these rules is iterated through, based on the color of the cell on which the ant lands. Landing on an “off” cell causes the ant to move according to the next rule. Landing on an “on” cell causes the ant to move according to the previous rule. If I implement multiple “on” colors, then I can cut the movement rules down to 6, but I will need to have each rule account for the color of the cell in which the ant currently resides.
Look for more iterations on this problem in days to come.
Langton’s Ant – Hex pattern
Click here to see it running.
Mostly similar to the previous Langton’s Ant experiment, this one uses a hexagon-ish algorithm instead of a quad. Because I am using square pixels to draw the results, it isn’t precisely a hexagon, but it is close enough to get the point across. Actually, the “ant” view is quite a bit more interesting than the heatmap view.
Click the Flash movie to toggle between the views.