- Fifty of the Best Poetry Books from Modern Authors. I have, or have read, only five of these. I obviously have work to do.
- Fun Twitter thread UNPOPULAR OPINIONS: EPIC FANTASY.
- Tor.com’s list of genre books coming out in April 2019
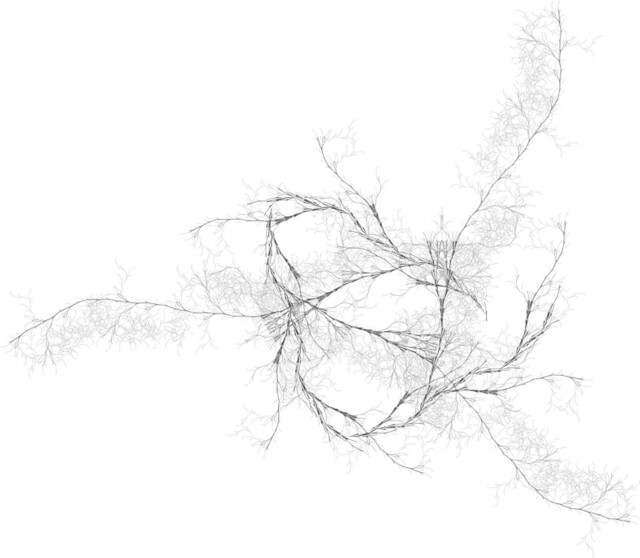
Over the past couple of weeks I have resurrected an old Flash experiment from back around, oh, 2007: The Lindenmayer Explorer. The image at the top of this post was created in the Explorer. Head over and check it out! If you create anything interesting, post it online and add a link in the comments here. Basic instructions are on the page. More detailed instructions and notes to follow.